normflows: A PyTorch Package for Normalizing Flows
normflows is a PyTorch implementation of discrete normalizing flows. Many popular flow architectures are implemented,
see the list below. The package can be easily installed via pip.
The basic usage is described here, and a full documentation
is available as well. A more detailed description of this package is given in our
accompanying paper.
Several sample use cases are provided in the
examples folder,
including Glow,
a VAE, and
a Residual Flow.
Moreover, two simple applications are highlighed in the examples section. You can run them
yourself in Google Colab using the links below to get a feeling for normflows.
| Link | Description |
|---|---|
| Real NVP applied to a 2D bimodal target distribution | |
| Modeling a distribution on a cylinder surface with a neural spline flow | |
| Modeling and generating CIFAR-10 images with Glow |
Implemented Flows
| Architecture | Reference |
|---|---|
| Planar Flow | Rezende & Mohamed, 2015 |
| Radial Flow | Rezende & Mohamed, 2015 |
| NICE | Dinh et al., 2014 |
| Real NVP | Dinh et al., 2017 |
| Glow | Kingma et al., 2018 |
| Masked Autoregressive Flow | Papamakarios et al., 2017 |
| Neural Spline Flow | Durkan et al., 2019 |
| Circular Neural Spline Flow | Rezende et al., 2020 |
| Residual Flow | Chen et al., 2019 |
| Stochastic Normalizing Flow | Wu et al., 2020 |
Note that Neural Spline Flows with circular and non-circular coordinates are supported as well.
Installation
The latest version of the package can be installed via pip
pip install normflows
At least Python 3.7 is required. If you want to use a GPU, make sure that PyTorch is set up correctly by following the instructions at the PyTorch website.
To run the example notebooks clone the repository first
git clone https://github.com/VincentStimper/normalizing-flows.git
and then install the dependencies.
pip install -r requirements_examples.txt
Usage
A normalizing flow consists of a base distribution, defined in
nf.distributions.base,
and a list of flows, given in
nf.flows.
Let's assume our target is a 2D distribution. We pick a diagonal Gaussian
base distribution, which is the most popular choice. Our flow shall be a
Real NVP model and, therefore, we need
to define a neural network for computing the parameters of the affine coupling
map. One dimension is used to compute the scale and shift parameter for the
other dimension. After each coupling layer we swap their roles.
import normflows as nf
# Define 2D Gaussian base distribution
base = nf.distributions.base.DiagGaussian(2)
# Define list of flows
num_layers = 32
flows = []
for i in range(num_layers):
# Neural network with two hidden layers having 64 units each
# Last layer is initialized by zeros making training more stable
param_map = nf.nets.MLP([1, 64, 64, 2], init_zeros=True)
# Add flow layer
flows.append(nf.flows.AffineCouplingBlock(param_map))
# Swap dimensions
flows.append(nf.flows.Permute(2, mode='swap'))
Once they are set up, we can define a
nf.NormalizingFlow
model. If the target density is available, it can be added to the model
to be used during training. Sample target distributions are given in
nf.distributions.target.
# If the target density is not given
model = nf.NormalizingFlow(base, flows)
# If the target density is given
target = nf.distributions.target.TwoMoons()
model = nf.NormalizingFlow(base, flows, target)
The loss can be computed with the methods of the model and minimized.
# When doing maximum likelihood learning, i.e. minimizing the forward KLD
# with no target distribution given
loss = model.forward_kld(x)
# When minimizing the reverse KLD based on the given target distribution
loss = model.reverse_kld(num_samples=512)
# Optimization as usual
loss.backward()
optimizer.step()
Examples
We provide several illustrative examples of how to use the package in the
examples
directory. Among them are implementations of
Glow,
a VAE, and
a Residual Flow.
More advanced experiments can be done with the scripts listed in the
repository about resampled base distributions,
see its experiments
folder.
Below, we consider two simple 2D examples.
Real NVP applied to a 2D bimodal target distribution
In this notebook, which can directly be opened in Colab, we consider a 2D distribution with two half-moon-shaped modes as a target. We approximate it with a Real NVP model and obtain the following results.
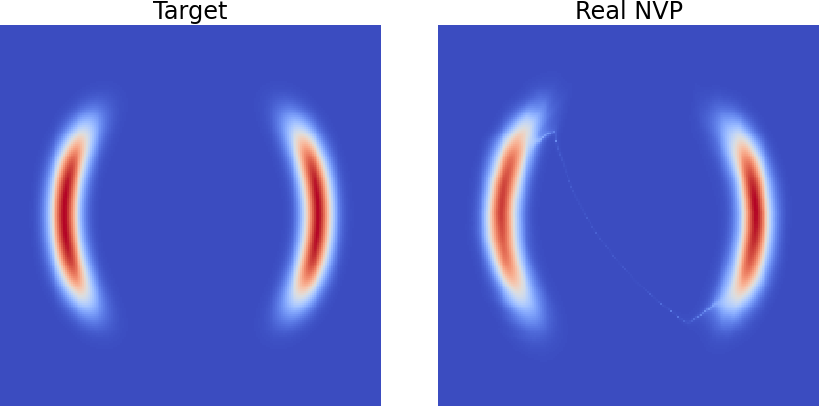
Note that there might be a density filament connecting the two modes, which is due to an architectural limitation of normalizing flows, especially prominent in Real NVP. You can find out more about it in this paper.
Modeling a distribution on a cylinder surface with a neural spline flow
In another example, which is available in Colab as well, we apply a Neural Spline Flow model to a distribution defined on a cylinder. The resulting density is visualized below.
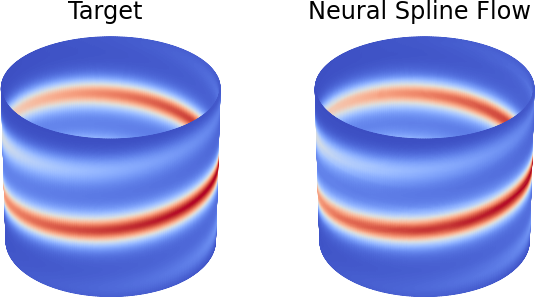
This example is considered in the paper accompanying this repository.
Support
If you have problems, please read the package documentation and check out the examples section above. You are also welcome to create issues on GitHub to get help. Note that it is worthwhile browsing the existing open and closed issues, which might address the problem you are facing.
Contributing
If you find a bug or have a feature request, please file an issue on GitHub.
You are welcome to contribute to the package by fixing the bug or adding the feature yourself. If you want to
contribute, please add tests for the code you added or modified and ensure it passes successfully by running pytest.
This can be done by simply executing
pytest
within your local version of the repository. Make sure you code is well documented, and we also encourage contributions to the existing documentation. Once you finished coding and testing, please create a pull request on GitHub.
Used by
The package has been used in several research papers. Some of them are listed below.
Andrew Campbell, Wenlong Chen, Vincent Stimper, José Miguel Hernández-Lobato, and Yichuan Zhang. A gradient based strategy for Hamiltonian Monte Carlo hyperparameter optimization. In Proceedings of the 38th International Conference on Machine Learning, pp. 1238–1248. PMLR, 2021.
Vincent Stimper, Bernhard Schölkopf, and José Miguel Hernández-Lobato. Resampling Base Distributions of Normalizing Flows. In Proceedings of The 25th International Conference on Artificial Intelligence and Statistics, volume 151, pp. 4915–4936, 2022.
Laurence I. Midgley, Vincent Stimper, Gregor N. C. Simm, Bernhard Schölkopf, and José Miguel Hernández-Lobato. Flow Annealed Importance Sampling Bootstrap. The Eleventh International Conference on Learning Representations, 2023.
Arnau Quera-Bofarull, Joel Dyer, Anisoara Calinescu, J. Doyne Farmer, and Michael Wooldridge. BlackBIRDS: Black-Box Inference foR Differentiable Simulators. Journal of Open Source Software, 8(89), 5776, 2023.
Utkarsh Singhal, Carlos Esteves, Ameesh Makadia, and Stella X. Yu. Learning to Transform for Generalizable Instance-wise Invariance. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pp. 6211-6221, 2023.
Ba-Hien Tran, Giulio Franzese, Pietro Michiardi, and Maurizio Filippone. One-Line-of-Code Data Mollification Improves Optimization of Likelihood-based Generative Models. Advances in Neural Information Processing Systems 36, pp. 6545–6567, 2023.
Moreover, the boltzgen package
has been build upon normflows.
Citation
If you use normflows, please cite the
corresponding paper as follows.
Stimper et al., (2023). normflows: A PyTorch Package for Normalizing Flows. Journal of Open Source Software, 8(86), 5361, https://doi.org/10.21105/joss.05361
Bibtex
@article{Stimper2023,
author = {Vincent Stimper and David Liu and Andrew Campbell and Vincent Berenz and Lukas Ryll and Bernhard Schölkopf and José Miguel Hernández-Lobato},
title = {normflows: A PyTorch Package for Normalizing Flows},
journal = {Journal of Open Source Software},
volume = {8},
number = {86},
pages = {5361},
publisher = {The Open Journal},
doi = {10.21105/joss.05361},
url = {https://doi.org/10.21105/joss.05361},
year = {2023}
}


